OpenMP 笔记 Pt.I

Table of Contents

(一共两篇，这是第一篇)

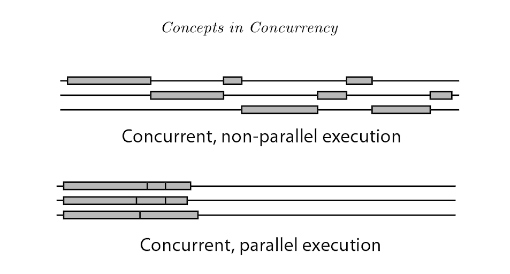
1. Concurrency VS Parallelism

1.1. 定义

  • Concurrency(并行): CPU 一次性 处理(logically active) 多个任务的能力

    [A property of execution flows]

  • Parallelism(并发): 多个 CPU 同时 运行(actually active) 多个任务的能力

    [A State of execution flows]

1.2. 图例

para.jpg

2. OpenMP: 一个开发多线程程序的 API

2.1. 基本信息

OpenMP construct 大部分是编译器指令，格式为: 

#pragma omp construct [clause [clause]…]

其中，函数原型等定义在 omp.h 中 

#include <omp.h>

2.2. 使用 OpenMP

使用 gcc 时，只需要加上 -fopenmp 就可以启用 OpenMP 

gcc -fopenmp foo.c
export OMP_NUM_THREADS=4
./a.out

2.2.1. 第一个并发程序: Hello World   example

#include <omp.h> // OpenMP include file
#include <stdio.h>

int main()
{
    #pragma omp parallel num_threads(4) // Parallel region with 4 threads
    {
        int id = omp_get_thread_num(); // Runtime library function to return a thread ID
        printf("Hello World from thread = %d", id);
        printf(" with %d threads\n",omp_get_num_threads());
    } // End of the Parallel region
}

运行结果是: 

./a.out 
Hello World from thread = 0 with 4 threads
Hello World from thread = 1 with 4 threads
Hello World from thread = 3 with 4 threads
Hello World from thread = 2 with 4 threads

2.2.2. 线程的互动方式

2.2.2.1. 共享内存计算机
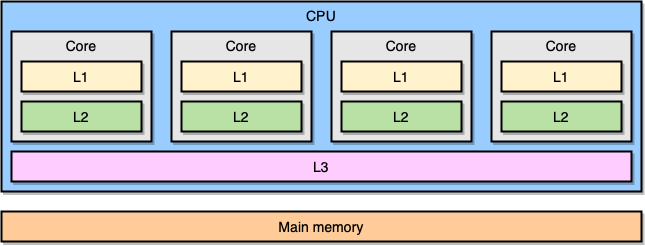
  • 对称多处理器 (SMP)

SMP 中，所有处理器共享相同的地址空间，每个处理器对内存的访问是"等时 (equal-time)"的，且操作系统以相同的方式对待每个处理器

  • 非一致性内存访问多处理器 (NUMA)

NUMA 中，内存被分成不同的区域: "近"内存和"远"内存 (远近指与特定处理器的物理距离), 处理器访问近内存的速度更快，而访问远内存的速度较慢

  1. What about CPU Cache?

    cache.png

    举个例子: Intel® Core™ i7-970

    • 它有6个核心，每个核心支持2路超线程
    • 它是一个6宽超标量处理器，能够在每个时钟周期发出6条指令，同时在3个管线中支持4宽 SIMD 操作
    • 它拥有192KB的L1缓存，1.5MB的L2缓存，以及12MB的共享L3缓存

    虽然它看起来像是一个SMP系统，但其缓存层次结构意味着不同核心对不同内存地址的访问成本是不同的，因此它实际上是NUMA

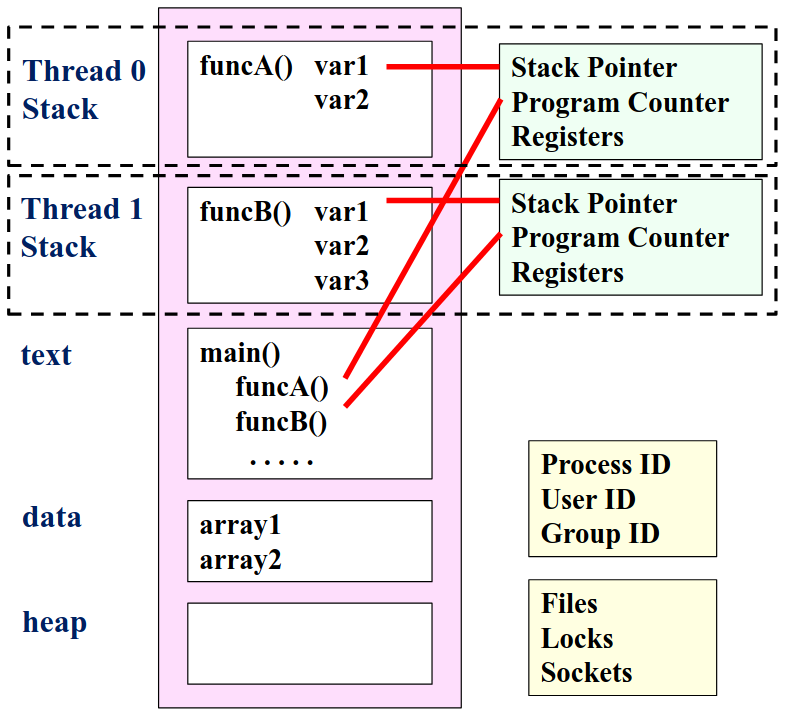
2.2.2.2. 单线程与多线程

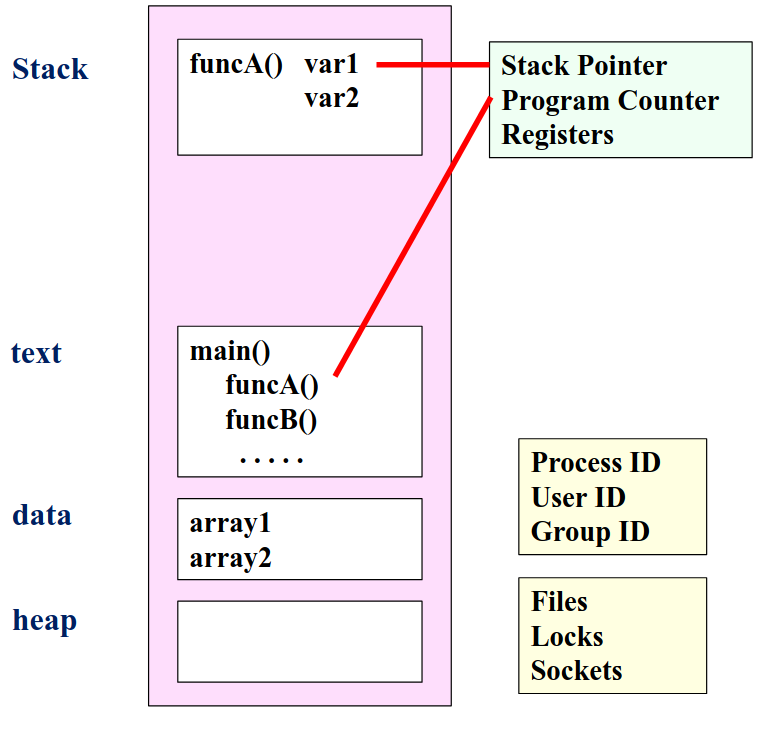
normal.png para.png

  • 单线程：所有执行都在一个栈上，内存结构更简单
  • 多线程：每个线程有自己的栈指针和 PC，允许并发执行

所以，对于一个程序:

  • 它有一个进程和很多个线程
  • 线程互动是通过对共享内存空间的读写操作
  • OS 的调度器决定线程的运行顺序
  • 多个线程可能同时访问共享数据，同步机制可以确保在任何时刻只有一个线程可以访问共享资源

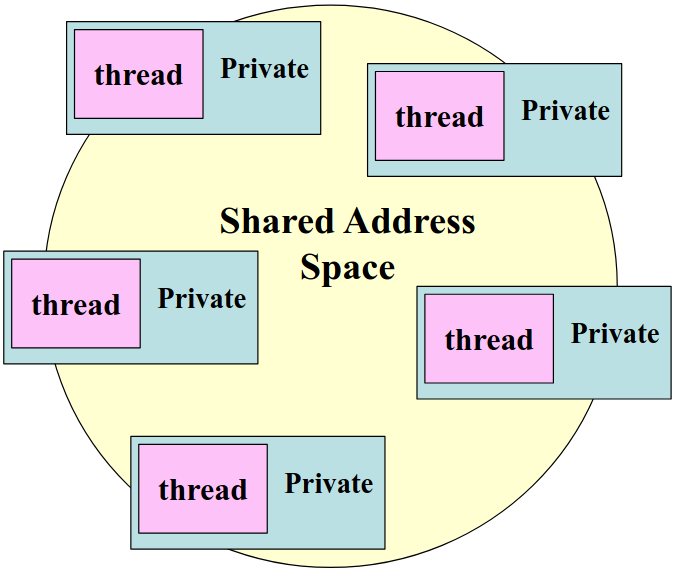
shared.png

2.2.3. OpenMP 的系统概述

OpenMP 是多线程共享地址模型

  • 线程通过共享变量进行通信

数据的意外共享会导致竞争：

  • 竞争条件：当程序的结果因线程调度的不同而发生变化

为了控制竞争条件：

  • 使用同步机制来保护数据冲突

由于同步开销较大，因此：

  • 最好改变数据的访问方式，以最小化对同步的需求

3. OpenMP 的功能探索

3.1. 创建线程

3.1.1. Fork-join 并行计算模型

  • 在 Fork-Join 模型中，通常有一个主线程，负责管理并行任务的执行

  • 当主线程需要进行并行计算时，它会分叉出一组子线程 

             master
       ----------
      /__________\
     / sequential \
-----              -----
     \ sequential /
       ----------

3.1.2. 在 OpenMP 中创建线程

  • 方法一
#include <omp.h> // OpenMP include file
#include <stdio.h>

int main()
{
    int a = 1;
    /* Each thread executes a copy of the
       code within the structured block*/
    omp_set_num_threads(4); //Runtime function to request a certain number of threads
    #pragma omp parallel
    {
        int id = omp_get_thread_num(); // Runtime library function to return a thread ID
        foo(a, id) // for ID = 0 to 3
    } // End of the Parallel region

    return 0;
}
  • 方法二
#include <omp.h> // OpenMP include file
#include <stdio.h>

int main()
{
    int a = 1;
    /* Each thread executes a copy of the
       code within the structured block*/
    #pragma omp parallel num_threads(4) // clause to request a certain number of threads
    {
        int id = omp_get_thread_num(); // Runtime library function to return a thread ID
        foo(a, id) // for ID = 0 to 3
    } // End of the Parallel region

    return 0;
}

3.1.3. 线程执行

         |
       a = 1
         |
         |
omp_set_num_threads(4)
         |--------|--------|--------|
      foo(a,0) foo(a,1) foo(a,2) foo(a,3) 
         |--------|--------|--------|
         | <-- Threads wait here for all threads to finish before proceeding (barrier)
      return 0
         |

3.1.4. 编译器在干什么?

考虑这个 construct: 

#pragma omp parallel num_threads(4)
{
    foo();
}

编译器会将它变成以下的程序: 

void thunk ()
{
    foo();
}

pthread_t tid[4];
for (int i = 1; i < 4; ++i)
    pthread_create (
        &tid[i],0,thunk, 0);
thunk();

for (int i = 1; i < 4; ++i)
    pthread_join (tid[i]);

OpenMP 使用线程池机制，所以在并行区域内，线程是从一个预先创建的线程池中获取的

在上例中，只有三个线程被创建，因为最后一个并行线程是由主线程调用的

3.1.5. 用 OpenMP 来优化定积分计算   example

考虑以下定积分:

\(\int_0^1 \frac{4.0}{(1 + x^2)} dx = \pi\)

根据定积分的几何意义，我们可以写出一个 naive 的计算实现: 

static long num_steps = 100000;
double step;
int main ()
{
    int i; double x, pi, sum = 0.0;
    step = 1.0/(double) num_steps;
    for (i=0;i< num_steps; i++)
    {
        x = (i+0.5)*step;
        sum = sum + 4.0/(1.0+x*x);
    }
    pi = step * sum;
}

接下来我们试着使用 OpenMP 来简单优化这个程序 

#include <omp.h>

static long num_steps = 100000;
double step;

#define NUM_THREADS 2

int main()
{
    int i, nthreads; double pi, sum[NUM_THREADS];
    step = 1.0/(double) num_steps;
    omp_set_num_threads(NUM_THREADS);

    #pragma omp parallel
    {
        int i, id, nthrds;
        double x;

        id = omp_get_thread_num();
        nthrds = omp_get_num_threads();
        if (id == 0) nthreads = nthrds;

        for (i=id, sum[id]=0.0;i< num_steps; i=i+nthrds)
        {
            x = (i+0.5)*step;
            sum[id] += 4.0/(1.0+x*x);
        }
    }
    for(i=0, pi=0.0;i<nthreads;i++)pi += sum[i] * step;
}

其中使用的一些技巧: 

int i, nthreads; double pi, sum[NUM_THREADS];

在这里将原先的标量 sum 提升为了一个有进程数个元素的 Array，以避免竞争

(每个线程都有自己独立的 sum[id] , 避免多个线程同时写入同一内存位置的情况。每个线程只更新自己对应的 sum 元素) 

for (i = id, sum[id] = 0.0; i < num_steps; i = i + nthrds)

循环分配 ：每个线程从自己的 id 开始，以 nthrds 为步长进行迭代，确保了每个线程处理不同的循环迭代，从而避免数据冲突

(a common trick in SPMD programs) 

if (id == 0) nthreads = nthrds;

针对全局变量的优化: nthreads 是一个全局变量，多个线程可能会同时写入它，导致竞争条件

于是在代码中，只允许一个线程来更新 nthreads , 从而避免多个线程同时写入同一地址

3.1.5.1. 什么是 SPMD ?

SPMD (Simple Program Multiple Data) 即单程序多数据的算法设计策略

Concepts

  • 单程序: 在 SPMD 模式下，所有核心运行相同的程序, which means 代码是统一的，所有处理单元执行相同的指令
  • 多数据: 每个处理单元处理不同的数据集，通过不同的输入数据，处理单元可以独立执行任务

Rank

处理单元都有一个标识符，称为 Rank，通常是从 0 到 P−1 的整数 (So P 是处理单元的数量)

3.1.6. 虚假共享: 对定积分程序再次优化

虚假共享是指多个线程在不同的内存位置上进行写操作时，这些内存位置恰好位于同一个缓存行中

现代处理器使用缓存来提高数据访问速度，当一个线程更新某个数据时，整个缓存行会被标记为无效，导致其他线程需要重新从主内存加载这个缓存行，从而引发性能下降

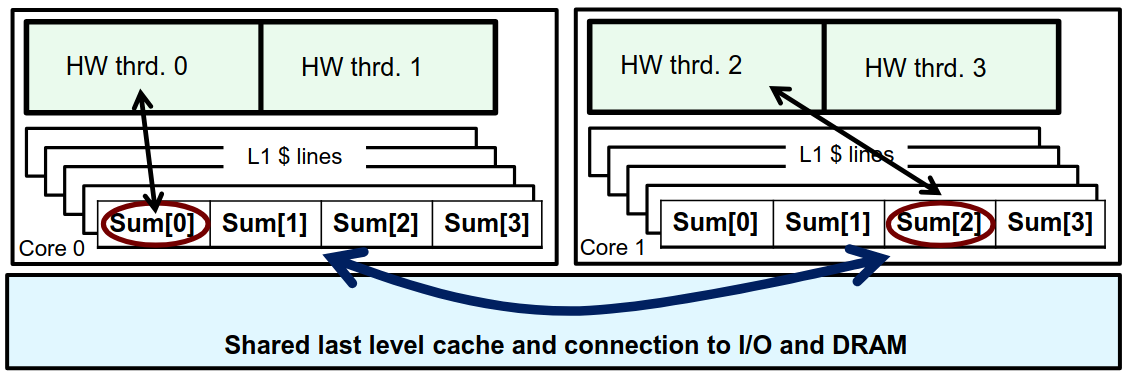
false.png

所以我们之前对 sum 的提升带来了很大的问题! 

double sum[NUM_THREADS];

数组的元素在内存中是连续存放的，这意味着它们可能会共享同一个缓存行 (尤其是在数组元素较小的情况下)

3.1.6.1. 那怎么办? 填充数组!

如果我们通过某种方式使得数组的元素之间有足够的空间，确保每个元素位于不同的缓存行中

那么，每个线程在更新自己的数据时，就不会干扰到其他线程的数据

具体来说，在数组中插入额外的空元素就可以 (就这么简单…) 

#include <omp.h>

static long num_steps = 100000;
double step;

#define NUM_THREADS 2
#define PAD 8 // assume 64 byte L1 cache line size
int main()
{
    int i, nthreads; double pi, sum[NUM_THREADS][PAD];
    step = 1.0/(double) num_steps;
    omp_set_num_threads(NUM_THREADS);

    #pragma omp parallel
    {
        int i, id, nthrds;
        double x;

        id = omp_get_thread_num();
        nthrds = omp_get_num_threads();
        if (id == 0) nthreads = nthrds;

        for (i=id, sum[id]=0.0;i< num_steps; i=i+nthrds)
        {
            x = (i+0.5)*step;
            sum[id][0] += 4.0/(1.0+x*x);
        }
    }
    for(i=0, pi=0.0;i<nthreads;i++)pi += sum[i][0] * step;
}

问题圆满解决…了吗?

填充数组需要CPU架构相关的知识，学习成本高；其次，如果程序被移植到缓存行大小不同的CPU上，那么优化就有可能变成负优化…

3.2. 同步机制

之前在 OpenMP 的系统概述中提到:

为了控制竞争条件：

  • 使用同步机制来保护数据冲突

所以使用同步机制可以用一个 universal 的方式解决之前遇到的问题

3.2.1. 两种最常见的同步方式

  • Mutual Exclusion

当一个线程想要进入可以访问共享资源的代码块时，它必须首先获得锁
一旦获得锁，其他线程就无法进入临界区，直到持有锁的线程释放它

  • Barrier

Barrier 要求所有参与的线程在某个特定点上停下来，直到所有线程都到达这个点 

         |
       a = 1
         |
         |
omp_set_num_threads(4)
         |--------|--------|--------|
      foo(a,0) foo(a,1) foo(a,2) foo(a,3) 
         |--------|--------|--------|
         | <-- Threads wait here for all threads to finish before proceeding (barrier)
      return 0
         |

3.2.2. 其他的同步方式/一些例子

3.2.2.1. 高阶同步
  • critical
  • atomic
  • barrier
  • ordered
3.2.2.2. 底层同步
  • flush
  • locks
3.2.2.3. Barrier
#pragma omp parallel
{
    int id=omp_get_thread_num();
    A[id] = foo1(id);
#pragma omp barrier // stops here
    B[id] = foo2(id, A);
}
3.2.2.4. Critical (Mutual Exclusion)
float res;
#pragma omp parallel
{
    float B; int i, id, nthrds;
    id = omp_get_thread_num();
    nthrds = omp_get_num_threads();
    for (i=id;i<niters;i+=nthrds)
    {
        B = big_job(i);
#pragma omp critical // Threads wait for their turns
        res += consume (B);
    }
}
3.2.2.5. Atomic (Mutual Exclusion)

Atomic 是一种特殊的同步机制，当多个线程需要对同一个变量进行更新时，使用 Atomic 可以确保每次更新都是安全的 

#pragma omp parallel
{
    double tmp, B;
    B = DOIT();  
    tmp = foo1(B);  
    #pragma omp atomic
    X += tmp;
}

在 OpenMP 中，Atomic 中的语句必须是以下几种形式之一：

  • x binop= expr
  • x++ : 自增操作
  • ++x : 前置自增
  • x-- : 自减操作
  • --x : 前置自减

3.2.3. 利用同步机制优化定积分程序

3.2.3.1. Critical
#include <omp.h>

static long num_steps = 100000;
double step;

#define NUM_THREADS 2

int main()
{
    int i, nthreads; double pi;
    step = 1.0/(double) num_steps;
    omp_set_num_threads(NUM_THREADS);

#pragma omp parallel
    {
        int i, id, nthrds;
        double x, sum;
        // Create a scalar local to each thread to accumulate partial sums

        id = omp_get_thread_num();
        nthrds = omp_get_num_threads();
        if (id == 0) nthreads = nthrds;

        for (i=id, sum=0.0;i< num_steps; i=i+nthrds)
        {
            x = (i+0.5)*step;
            sum += 4.0/(1.0+x*x);
        }
#pragma omp critical
        pi += sum * step;
    //Must protect summation into pi in a critical region so updates don’t conflict
    }
}
3.2.3.2. Atomic
#include <omp.h>

static long num_steps = 100000;
double step;

#define NUM_THREADS 2

int main()
{
    int i, nthreads; double pi;
    step = 1.0/(double) num_steps;
    omp_set_num_threads(NUM_THREADS);

#pragma omp parallel
    {
        int i, id, nthrds;
        double x, sum;
        // Create a scalar local to each thread to accumulate partial sums

        id = omp_get_thread_num();
        nthrds = omp_get_num_threads();
        if (id == 0) nthreads = nthrds;

        for (i=id, sum=0.0;i< num_steps; i=i+nthrds)
        {
            x = (i+0.5)*step;
            sum += 4.0/(1.0+x*x);
        }
        sum = sum * step;
#pragma omp critical
        pi += sum;
    //Must protect summation into pi in a critical region so updates don’t conflict
    }
}

添加同步机制的代码块时，需要小心逻辑错误，例如上面两个情况中，如果将最后的求和放入循环内部会导致读写冲突 (Use your brain)

3.2.4. SMPD vs. Worksharing

先前我们提到了 SMPD 单程序多数据的设计思想，但还有另外一个想法叫做 Worksharing，顾名思义便是共享线程之间工作，避免某些线程过载而其他线程空闲的情况发生

core.jpg

3.2.5. Worksharing constructs

OpenMP 为 C/C++ 提供了 for 作为 Loop construct name 

#pragma omp parallel
{
#pragma omp for
    for (I=0;I<N;I++)
    {
        foo(I);
    }
}

默认情况下，变量 I 是 private 的，也可以通过 private(I) 来显式声明这一点

3.2.5.1. 有什么用?

少写就是赢!

  • 未优化的代码:
for(i=0;i<N;i++) { a[i] = a[i] + b[i];}
  • 只用 parallel 优化的代码:
#pragma omp parallel
{
    int id, i, Nthrds, istart, iend;
    id = omp_get_thread_num();
    Nthrds = omp_get_num_threads();
    istart = id * N / Nthrds;
    iend = (id+1) * N / Nthrds;
    if (id == Nthrds-1)iend = N;
    for(i=istart;i<iend;i++) { a[i] = a[i] + b[i];}
}
  • 使用 Worksharing Loops 优化的代码
#pragma omp parallel
#pragma omp for
for(i=0;i<N;i++) { a[i] = a[i] + b[i];}

代码复杂度和长度直线下降，而且优化后的代码非常符合直觉

3.2.5.2. 调度子句

调度子句影响循环迭代如何映射到线程上

  • schedule(static [,chunk])

将循环的迭代静态地分配给线程，分配的块大小由参数 chunk 指定；每个线程获得一个固定大小的迭代块，直到所有迭代都被分配 

#pragma omp for schedule(static, 10)
for (int i = 0; i < N; i++) {
    // 处理十个迭代
}
  • schedule(dynamic [,chunk])

每个线程在完成其当前任务后，会去获取下一个任务，这样可以更好地适应迭代时间不均匀的情况 

#pragma omp for schedule(dynamic, 5)
for (int i = 0; i < N; i++) {
    // 每个线程处理5个迭代，动态获取
}
  • schedule(guided [,chunk])

线程动态地抓取迭代块，块的大小从大到小逐渐减小，直到达到 chunk 的大小 

#pragma omp for schedule(guided, 10)
for (int i = 0; i < N; i++) {
    // 每个线程动态获取迭代块，块大小逐渐减小
}
  • schedule(auto)

抛弃大脑让程序自己选 

#pragma omp for schedule(auto)
for (int i = 0; i < N; i++) {
    // 调度策略由运行时决定
}
  1. 适用范围
    调度子句 适用情况
    static 工作量预先确定
    dynamic 工作量不均衡，难预测
    guided 在 dynamic 基础上进一步减小开销
    auto 让运行时根据先前执行的经验自动选择

3.2.6. Working with Loops

在 OpenMP 中，以下两端代码是等价的: 

double res[MAX]; int i;
#pragma omp parallel
{
#pragma omp for
    for (i=0;i< MAX; i++)
    {
        res[i] = huge();
    }
}

double res[MAX]; int i;
#pragma omp parallel for
for (i=0;i< MAX; i++)
{
    res[i] = huge();
}
3.2.6.1. 方法论

  • 找到占用大量计算资源的循环

    可以使用性能分析工具如 perf 和 gprof

  • 拆分循环，防止循环依赖的情况发生

    如果存在依赖，可以使用临时变量或者修改算法来消除

  • 最后添加 OpenMP 指令

例如对于这个简单的循环: 

int i, j, A[MAX];
j = 5;
for (i=0;i< MAX; i++)
{
    j+=2;
    A[i] = big(j);
}

在这段代码中，循环中一个依赖 j , 如果直接添加 OpenMP 指令，那么可能会有多个线程希望同时访问 j 的情况发生，造成性能下降

所以针对这个情况，优化应该这样进行: 

int i, A[MAX];
#pragma omp parallel for
for (i=0;i< MAX; i++)
{
    int j = 5 + 2*(i+1);
    A[i] = big(j);
}
3.2.6.2. 特殊情况之: 嵌套循环

对于嵌套循环，可以使用 collapse(n) 来让 OpenMP 进行优化: 

#pragma omp parallel for collapse(2)
for (int i=0; i<N; i++)
{
    for (int j=0; j<M; j++)
    {
        ......
    }
}

原理 : 使用 collapse(2) 将两个循环合并为一个单一的循环，形成一个长度为 N×M 的循环

3.2.6.3. 特殊情况之: 规约

考虑以下求均值的程序: 

double ave=0.0, A[MAX]; int i;
for (i=0;i< MAX; i++)
{
    ave + = A[i];
}
ave = ave/MAX;

在这个程序中，每个循环迭代的结果依赖于前一个迭代的累积结果，这种依赖性使得我们不能简单地并行化这个循环

OpenMP 提供了对归约操作的支持，可以通过在并行化指令中添加 reduction 子句来处理归约操作

语法 : reduction (op : list)

以上程序可以优化为: 

double ave = 0.0, A[MAX];
#pragma omp parallel for reduction (+:ave)
for (int i = 0; i < MAX; i++)
{
    ave += A[i];
}
ave = ave / MAX;

原理 :

  • 对于列表中的每个变量，OpenMP会为每个线程创建一个 local copy，并根据操作类型进行初始化，例如，使用 0 初始化用于 +，使用 1 初始化用于 *
  • 每个线程在其局部副本上进行操作，例如，在加法归约中，线程会将数组 A 的元素加到它的局部副本中
  • 当所有线程完成计算后，OpenMP会将每个local copy的结果合并为一个单一值，与原始的全局变量结合

Author: mitchell

Created: 2025-01-24 Fri 13:18

This webpage is generated by GNU Emacs